Composing Your Own Transformation Matrix

navigation bar

Table of Contents > QUARC > User's Guide > Creating User Interfaces > Creating Visualizations

The Visualization Set Variables blocks let you set the translation, orientation (using roll, pitch, yaw), and scale with separate ports. If you want complete control in order to change frames (without using dummy actors), or you want access to the bottom row of the transformation matrix to control perspective, skew, and shear, then you can create your own transformation matrix.

The Matrix Contents

A homogeneous matrix is typically divided into the rotation matrix and the translation vector and scale is embedded into the rotation matrix. The most basic matrix that you can input into a Set Variables block is an identity matrix:

Identity matrix.

By multiplying this identity matrix by a homogeneous rotation matrix,

Rotation matrix.

translation matrix,

Translation matrix.

or scale matrix

Scale matrix.

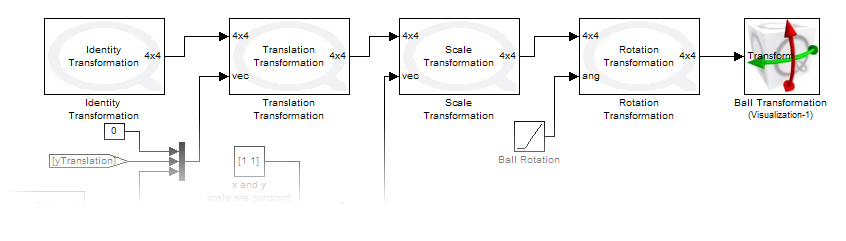
in the appropriate order, you can achieve any transformation you wish. To help you do this in the Simulink environment are the identity matrix, rotation transformation, scale transformation, and translation transformation blocks found in the QUARC Targets/Math Operations/Homogeneous Transformations library. Beginning with an identity matrix (just a masked constant block with eye(4)), feed the output of each block to the input of the next in the order that achieves the desired transformation. Double clicking on the transformation blocks gives you the option of changing between fixed transformations, or variable transformations from an external control input. The final output can be used to drive a Set Variables block or for further analysis as shown below.

Composing your own transformation matrix with the homogeneous blocks.

Warning

Unlike the Scale input on the Set Variables block, the scale transformation block will not prevent you from using a scale of zero. It is your responsibility to ensure that the determinant of the transformation matrix is not zero, otherwise the results of the visualization may not be as expected.

An example of using the transformation blocks can be found in the Visualization Homogeneous Transform Demo. The demo contains an example of an ordering of transformations that would otherwise require a number of dummy actors to achieve.

navigation bar